H-DES: A Quantum-Classical Hybrid Differential Equation Solver

We are excited to announce that as of October 2, 2024, we,ColibriTD, have published our Quantum-Classical Hybrid Differential Equation Solver[1] (H-DES) on arXiv (https://arxiv.org/abs/2410.01130). H-DES represents three years of dedicated research and development by our R&D team and has already been utilized in several collaborative projects with our partners, including Eviden and Onera. Today, after extensive testing and validation, we are submitting it for publication with confidence in its practical applications.

What is H-DES?

H-DES is a hybrid quantum-classical algorithm designed to solve systems of differential equations (DEs) and partial differential equations (PDEs). Like other solutions emerging in the NISQ (Noisy Intermediate-Scale Quantum) era, H-DES leverages Variational Quantum Algorithms (VQA). In this approach, the solution to a differential equation is encoded via a spectral decomposition in the expectation value of a quantum state, which is generated by a Variational Quantum Circuit (VQC). By measuring this VQC, we obtain an estimate of both the solution and its derivatives for a given set of parameters.

These measurements are compared to the physical problem, i.e., the DE or PDE we aim to solve, along with the relevant boundary conditions. This comparison defines a loss function that is minimized by a classical optimizer. The optimizer then provides a new set of parameters for the VQC, forming what we call the Hybrid Loop (see Figure 1).

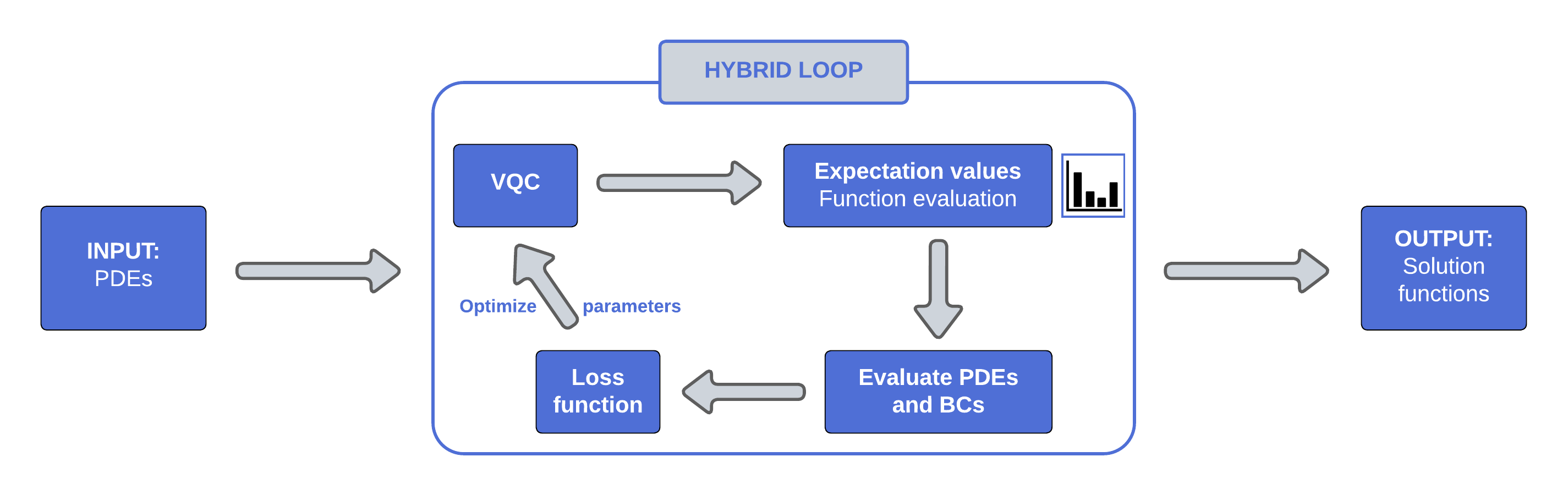
What makes H-DES unique?

H-DES shares common ground with other VQC-based solutions in that only a limited number of qubits and reasonable depth is required to explore an exponentially large Hilbert space. In H-DES this feature translates to a high precision in the solution function. Additionally, the number of parameters to optimize scales linearly and not exponentially with the number ofqubits. What sets H-DES apart is its use of spectral decomposition,which is handled through the definition of measurement observables. This eliminates the need for specific feature maps for the function and its derivatives, a common practice in VQC and Quantum Machine Learning techniques. As a result, H-DES reduces the number of quantum circuits required and avoids derivative approximations, both of which are significant improvements for the current generation of noisy quantum computers.

Toward a Universal Differential Equation Solver

H-DES is designed to handle a wide range of differential equations, including linear, non-linear, partial, and coupled DEs. It will serve as a corner stone of our quantum computing platform, Quick. Our team is currently exploring various use cases, ranging from material deformation to combustion and fluid dynamics.

To ensure H-DES operates effectively in noisy quantum environments, we are also advancing techniques such as optimized initialization strategies and error mitigation methods. While this is only the beginning, we look forward to sharing concrete applications of H-DES in the near future.

[1]H-DES is subject to a patent submission (EP24306601). Use of this method requires alicense, which can be obtained from ColibriTD.

‍